📈 The Mathematics of Pareto Optimality: A Deep Dive into Efficiency

Imagine you’re dividing a cake between two people. If you cut it in a way that gives one person a larger piece without making the other’s smaller, most of us would agree that’s an improvement. But eventually, you’ll reach a point where making one person happier requires making the other worse off. That’s when you’ve hit something economists call Pareto optimality.

This concept, named after the Italian economist Vilfredo Pareto, sits at the heart of welfare economics and resource allocation theory. It’s often used to evaluate policies, negotiations, and trade-offs in multi-agent systems. But what does it really mean — mathematically? That’s what we’re diving into here.

Understanding the Core Idea

In everyday terms, a situation is Pareto optimal if there’s no way to make someone better off without making someone else worse off. It’s not about fairness, equality, or even maximizing happiness. It’s simply about efficiency — about exhausting all win-win possibilities.

In economics, we typically represent people's well-being with utility functions. If there are two individuals, their utilities can be plotted on a graph: one person’s utility on the horizontal axis, the other’s on the vertical. Every possible allocation of resources corresponds to a point in this space. The collection of all achievable utility combinations forms what’s known as the feasible set.

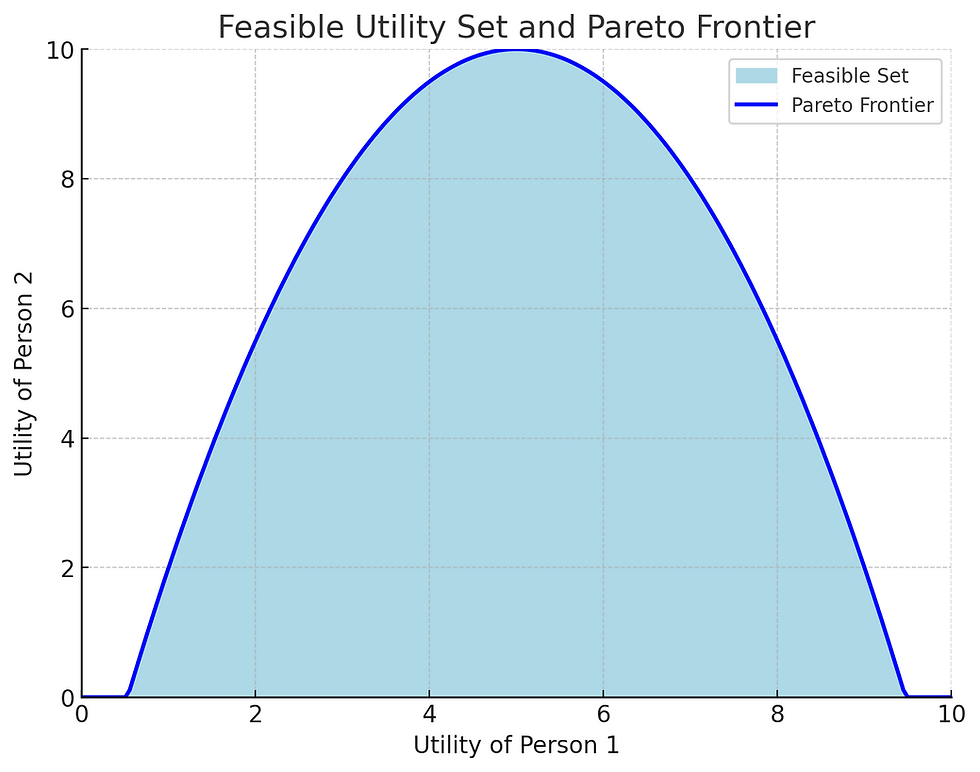
Now imagine tracing the outer boundary of this set, where you can’t move further in one direction without losing ground in another. That edge is the Pareto frontier. Points along this frontier are Pareto optimal. Any point inside the feasible set, by contrast, is suboptimal because someone can be made better off without harming anyone else.

The Formal Definition

Mathematically, suppose we have nn individuals, each with a utility function. A utility allocation is just a vector (u1,u2,…,un)(u1​,u2​,…,un​), and the set of all such attainable allocations—given the constraints of the economy—is denoted UU.

An allocation U∗∈UU∗∈U is Pareto optimal if there is no other U∈UU∈U such that every individual is at least as well off, and at least one is strictly better off. If such an alternative existed, the original allocation would be inefficient, because a Pareto improvement was still possible.

In two dimensions, this condition is easy to visualize. Suppose you’re standing inside the feasible set. If you can move up or to the right without leaving the set, someone’s utility can be increased while the other's remains constant or even increases. But once you’re on the edge of the set, any further improvement for one person necessarily involves loss for the other. That’s Pareto optimality in action.

Beyond Two People

With more individuals, the utility space becomes multi-dimensional, and the Pareto frontier turns into a Pareto surface—a more abstract, but conceptually similar, boundary. You can no longer visualize it easily, but the logic remains intact. Mathematicians and economists use tools like convex analysis, optimization theory, and utility-possibility frontiers to study the structure of this surface.

In optimization terms, Pareto optimality shows up in multi-objective problems, where you’re trying to optimize several functions at once. Think of designing a product: you want it to be cheap, durable, and attractive. Improving one objective often comes at the expense of another. The set of solutions where you can’t improve one criterion without worsening another forms the Pareto frontier.

Efficiency ≠ Equity

It’s important to stress that Pareto optimality says nothing about fairness. A distribution where one person owns everything and everyone else has nothing can still be Pareto optimal, as long as there’s no way to improve someone’s lot without hurting the owner. That’s why many economists supplement Pareto analysis with social welfare functions that incorporate justice or equity explicitly.

Pareto efficiency is also not unique. There are usually many different Pareto optimal points, and societies must choose among them. Do we favor equality? Reward to effort? Need? Each ethical stance suggests a different "best" point along the frontier.

Real-World Relevance

Pareto optimality may sound abstract, but it shows up all the time. In public policy, when a government considers a reform—say, a tax change—it might help some people and hurt others. If it improves one group’s well-being without harming another, it’s a Pareto improvement. If it helps some and hurts others, it’s not. But just because a policy isn’t Pareto improving doesn’t mean it’s bad—after all, virtually all real reforms help some and harm others. That’s why economists often use broader concepts like Kaldor-Hicks efficiency, which allows for hypothetical compensation.

In engineering and design, Pareto optimality is used to manage trade-offs between competing goals—like power vs. battery life in mobile devices. In healthcare, it guides decisions about how to allocate limited resources. Even in everyday negotiations, the idea helps explain when deals can be struck and when we’re at an impasse.

Wrapping Up

The mathematics of Pareto optimality gives us a precise way to talk about efficiency in systems with multiple agents or objectives. It defines the boundary of what’s possible, given limited resources and competing interests. But it's only one tool in the economist's kit—powerful for analyzing trade-offs, but silent on questions of justice, power, or morality.

Understanding where the Pareto frontier lies is the first step. Deciding where we should be on that frontier? That’s the hard part.